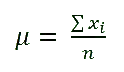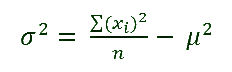FIRST HALF
This time,
Matifutbol has brought together some of the best football players to wish you a Happy 2014!
Thank you very much, but.... have you noticed that there are 13 players on your card? What a bad luck! Also, as year 2014 is coming, I think you should have invited 14 players for the photo.

Well, I can't see why number 13 has to mean bad luck. In any case, we can easily modify the card.
Yes? How? It will be difficult to gather them back to take a new picture with one more player...
There's a way to do it without putting them together again, using a translational move.
Can you imagine how?
SECOND HALF
Well, I can't imagine how to solve it...
In fact, there's nothing to solve. Number 13 is just a normal number, like any other.
Yes, but it's said to bring back luck. There must be something bad in it...
The truth is that this is something that comes from old times. Actually, it's a superstition that comes from the times of our ancestors, who worshiped the forces of nature.
Has nature anything to do with number 13?
 Yes, a lot, especially the Moon. Our ancestors discovered that there were years with 12 new moons, and years with 13 moons. Actually, the average is 12.41 new moons per year. Before we set calendars with 12 months, we used calendar with 13 months, one of which was shorter than the others.
Yes, a lot, especially the Moon. Our ancestors discovered that there were years with 12 new moons, and years with 13 moons. Actually, the average is 12.41 new moons per year. Before we set calendars with 12 months, we used calendar with 13 months, one of which was shorter than the others.
This incomplete thirteenth moon, which caused an atypical month, with fewer days than the rest, gave more headaches than benefits to the shamans who had to handle the calendar to set their rituals and festivals, so they finally ended up by 'hating' this number.
That's how all started?
This explanation is very likely, because almost all ancient cultures and civilizations throughout the world share some background on this issue.
Thus, 13 is considered a damned number by the ancient Persians, where number 13 was identified with chaos. Zoroaster also identifies it with the devil, and in Norse mythology the god Loki, Lord of the lies, appears as the 13th god assistant to a fateful dinner (dinners and number 13 tend to be closely related).

Egyptians also reserved number 13 for the last stage of life, the death. This is also taken by Tarot, that also assigns the death card to this number.
And in Christianity we find numerous references. From the thirteenth guest at the Last Supper of Jesus Christ (Judas Iscariot), the man who betrayed him, to the thirteenth chapter of Apocalypsis, in which the coming of Antichrist is predicted.
In any case, we could find an endless number of negative references regarding any number you want. But clearly there's something special about this number 13 that makes us to fix more attention on it than on others.

Yes, it's true that many people has some superstitious misgivings about this number.
And some people even take it to the extreme. We talk about triskaidekaphobia, which consists of the extreme and irrational fear to the number 13. Thus, due to this phobia, we can find countries where there's no 13th floor in buildings, hotels with 13th floor used for service tasks, streets without number 13, airplanes without seats row number 13, or athletes who avoid wearing this number on their backs. In other cases, 13th floor is replaced by 12 bis, for example, and there are also computer programs that hop from version 12 to 14.
But all these issues are completely contrary to Mathematics, aren't they?
Yes, they are, but not at all. Numerology (which is the set of beliefs or traditions that aims to stablish a mystical relationship between numbers and living things, physical and spiritual forces) has always evolved in parallel with the development of Mathematics.

Actually, a famous mathematician as Pythagoras, developed in his time (V century BC) a whole study on the relationship between numbers and the laws of nature. And also scholars of Kabbalah studied such relations, or Eastern cultures, that assign to numbers certain properties and meanings.
But regardless of this, number 13, only for mathematical purposes, it's also a very interesting number.
13 is a prime number, that is, it's only divisible by one and itself. It's also the first emirp number, ie, if we write it backwards, 31, we have another prime number.
Moreover, it's one of the terms of the Fibonacci sequence, in which each number is obtained by adding the previous two:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
It belongs to a Pythagorean triple: 5, 12, 13. This means that they are 3 positive integers that satisfy the condition that a2+b2=c2, that is, that can be associated with the lenghts of the two legs/catheti and the hypotenuse of a right triangle. Moreover, it's a primitive Pythagorean triple, ie, the greatest common divisor of the 3 numbers is 1.
Also, there are only 13 Archimedean solids (excluding isomorphic forms). And 13 were the number of books Euclid wrote about Mathematics: 'The Elements'.

 And Fibonacci sequence, in which each term is the sum of the previous two, is found in many places in nature: in the reproductive rates of animals or viruses, in the distribution of leaves around the stem of the plants for better use of the sun light, in pinapples, in sunflowers seeds, in daisies seeds, in arms of spiral galaxies and hurricanes, in equinodermos bodies, or in the family tree of bees .... It has also many applications in computing and games theory. And in addition, any natural number can be written as the sum of a limited number of terms in the Fibonacci sequence, each one different from the others.
And Fibonacci sequence, in which each term is the sum of the previous two, is found in many places in nature: in the reproductive rates of animals or viruses, in the distribution of leaves around the stem of the plants for better use of the sun light, in pinapples, in sunflowers seeds, in daisies seeds, in arms of spiral galaxies and hurricanes, in equinodermos bodies, or in the family tree of bees .... It has also many applications in computing and games theory. And in addition, any natural number can be written as the sum of a limited number of terms in the Fibonacci sequence, each one different from the others.
But this will also happen with any number, such as number 14.
But 2013 is also the sum of three consecutive sphenic numbers:
Both have 8 divisors: 1, 3, 11, 33, 61, 183, 671, 2013 and 1, 2, 19, 38, 53, 106, 1007, 2014.
What's that of translation?
Yes, I want to see what you do with the players. So I click the video.
Yes, but the important thing is that the message itself has remained the same: Matifutbol wishes you a Happy new year 2014!

With numbers 5 and 563, 13 is one of the 3 known Wilson primes, ie, that satisfies the property that 132 divides (13-1)! + 1.
13 is a happy number, as you can see on this link. It's the third ordered Bell number or Fubini number (related to combinatorial). And we could add more properties.
And is this important? What good is it to be a prime number or to belong to the Fibonacci sequence, for example?
Prime numbers have recently become important in the issue of documental encryption. Plus they're considered as the foundation over which all other natural numbers are constructed.
 And Fibonacci sequence, in which each term is the sum of the previous two, is found in many places in nature: in the reproductive rates of animals or viruses, in the distribution of leaves around the stem of the plants for better use of the sun light, in pinapples, in sunflowers seeds, in daisies seeds, in arms of spiral galaxies and hurricanes, in equinodermos bodies, or in the family tree of bees .... It has also many applications in computing and games theory. And in addition, any natural number can be written as the sum of a limited number of terms in the Fibonacci sequence, each one different from the others.
And Fibonacci sequence, in which each term is the sum of the previous two, is found in many places in nature: in the reproductive rates of animals or viruses, in the distribution of leaves around the stem of the plants for better use of the sun light, in pinapples, in sunflowers seeds, in daisies seeds, in arms of spiral galaxies and hurricanes, in equinodermos bodies, or in the family tree of bees .... It has also many applications in computing and games theory. And in addition, any natural number can be written as the sum of a limited number of terms in the Fibonacci sequence, each one different from the others.But this will also happen with any number, such as number 14.
Don't believe so. Unlike number 13, which seems to be a rather unique number in mattematical terms, number 14 has some peculiarities hardly worth mentioning.
It's a square pyramidal number, that is, it's the result of the sum of the first 3 square numbers:
14 = 12+22+32
If we visualize these squares as layeres of spheres placed one above the other, this number represents a pyramid with a square base.
Number 14 is a discrete semiprime or biprime number, because it’s a natural
number which is the result of the product of two prime
numbers 14=2*7.
It's a Catalan number (related to combinatorial problems), it's a open meandric number (related to intersections of curves and lines), it's a Pell-Lucas number (belongs to a sequence of
numbers related to the approximation by rational numbers to the square root of
2), and it’s the maximum number of electrons that can fit in the f atomic sublevel.
All these
are important features, but less relevant and practical than number 13’s properties.
So it’s seems
that calling 13 players, not 14, has been a good idea. But, what can you tell
me numbers 2013 and 2014?
They're both sphenic numbers, ie, they are the product of 3 distinct prime factors
2013=3*11*61 and 2014=2*19*53
2013 = 665 (5*7*19) + 670 (2*5*67) + 678 (2*3*113)
Both have 8 divisors: 1, 3, 11, 33, 61, 183, 671, 2013 and 1, 2, 19, 38, 53, 106, 1007, 2014.
And none of them is neither a Fibonacci number, nor a Bell, Catalan, factorial, regular prime, or perfect number.
Regarding to happiness, we can say that number 2013 ís a happy number, while 2014 is not.
So there’s
not much difference between the 2 numbers... However, I still think I don’t like
the card with only 13 players.
For they
have all gone to their homes, and it will be hard to bring them all together again, I propose
an exercise of translation.
What's that of translation?
It’s a process by which each point of the plane is shifted to another point at a distance.
It’s a direct move with no change in direction, ie, all moved objects maintain
their shape, orientation and size, so that the translated images are identical
to the initial figures.
Okay, but I
don’t know what are you going to achieve with a simple movement of the players.
I’m not
changing only their places, but I 'm going to do something else. Do you want to
see it?
Yes, I want to see what you do with the players. So I click the video.
That’s a
really funny way to convert the 13 players in 14, but now some of them are not
recognizable...
Yes, but the important thing is that the message itself has remained the same: Matifutbol wishes you a Happy new year 2014!